yrl's blog
0%

JDK1.8 HashMap和ConcurrentHashMap 源码和实现

发表于 更新于 分类于

HashMap

AVL树：

在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。

特点：

1.本身首先是一棵二叉搜索树。

2.带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。

也就是说，AVL树，本质上是带了平衡功能的二叉查找树（二叉排序树，二叉搜索树）。

树的左旋：绕着子结点逆时针转动，如下图：

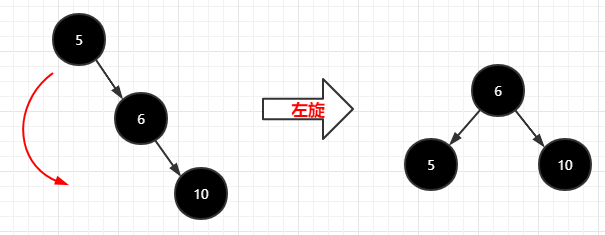
source-01

树的右旋：绕着子结点顺时针转动，如下图

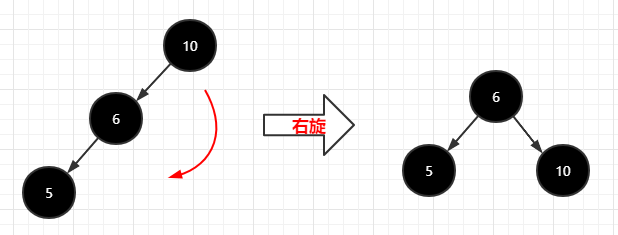
source-02

红黑树：

是一种自平衡二叉查找树，是一种特化的AVL树，都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。

它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的： 它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目。

若一棵二叉查找树是红黑树，则它的任一子树必为红黑树。红黑树是一种平衡二叉查找树的变体，它的左右子树高差有可能大于 1，所以红黑树不是严格意义上的平衡二叉树（AVL），但 对之进行平衡的代价较低， 其平均统计性能要强于 AVL 。

红黑树的实际应用非常广泛，比如Linux内核中的完全公平调度器、高精度计时器、ext3文件系统等等，各种语言的函数库如Java的TreeMap和TreeSet。

红黑树的定义如下：

1.每个结点是红的或者黑的

2.根结点是黑的

3.每个叶结点是黑的（每个结点有默认的黑色的NULL结点）

4.如果一个结点是红的，则它的两个儿子都是黑的（父子结点之间不能出现两个连续的红结点）

5.对每个结点，从该结点到其子孙结点的所有路径上包含相同数目的黑结点（黑色平衡）

在算法导论中，新插入的结点优先默认是红色的，优先满足第五条定义，再满足其他定义。

案例

1.假设现在插入一个根结点（10）

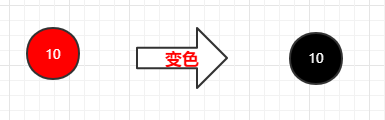
source-03

1
2
3
步骤：
1.先插入一个红色的结点，满足第五条定义
2.不满足第二条定义--->变色

2.再插入一个结点（20）

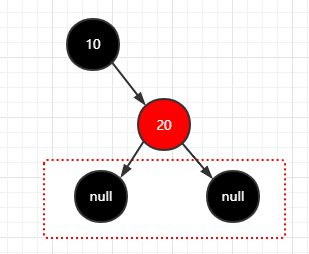
source-04

1
2
3
步骤：
1.先和根节点比大小，判断要落在根节点的右边
2.校验是否满足所有定义--->满足

这是一颗正常的红黑树。因为每个节点，它的末尾节点都有隐藏的黑色空节点，所以满足第三条定义。

再插入一个结点（30）

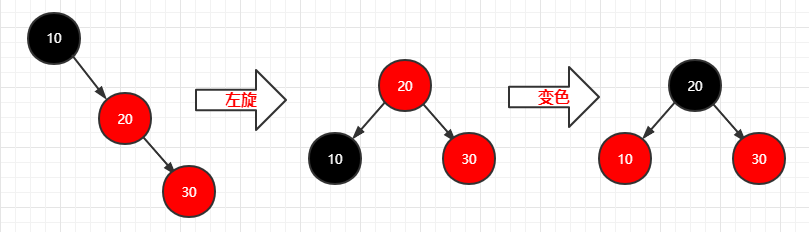
source-05

1
2
3
4
步骤：
1.插入节点后判断是否满足第五定义--->左旋
2.左旋后判断是否满足第二定义--->需要变色
3.旋转的结点和中心结点进行变色

再插入一个结点（40）

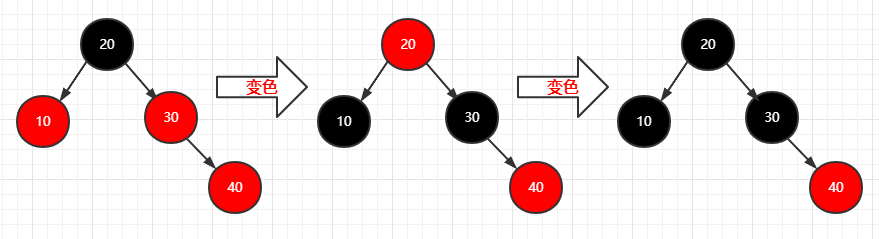
source-06

1
2
3
4
5
步骤：
1.插入结点后判断是否满足第四定义--->变色
2.判断是否满足第二定义--->变色
结论：
父节点是黑色的，则不需要调整

再插入两个结点（5）（25）

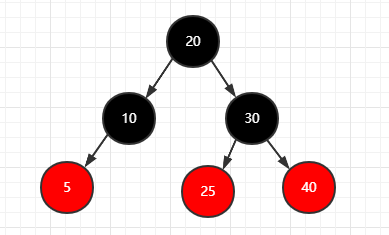
source-09

1
2
步骤：
父节点是黑色的，不需要调整

再插入一个结点（50）

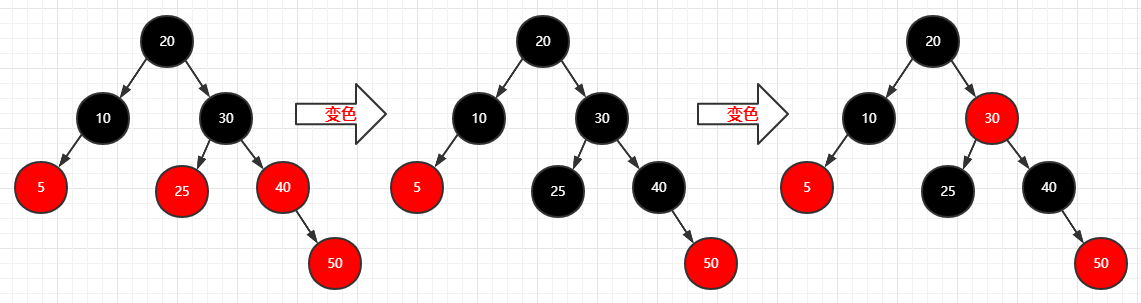
source-10

1
2
3
4
步骤：
1.父节点和叔叔节点变色
2.祖父节点变色
结论：父节点是红色时，叔叔节点也是红色时，则父节点和叔叔节点变色，祖父节点变色。

再插入两个结点（35）（60）

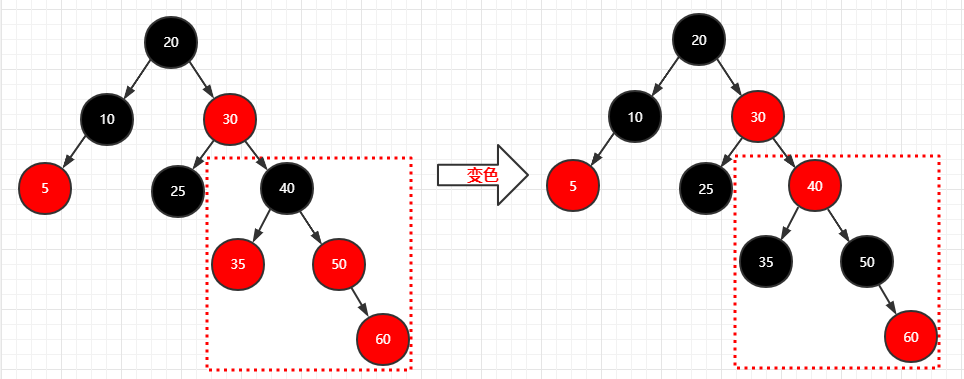
source-11

1
2
3
步骤：
1.先保证红框中的子树是一颗红黑树
2.按照上文案例的结论，父节点和叔叔节点变色，祖父节点变色

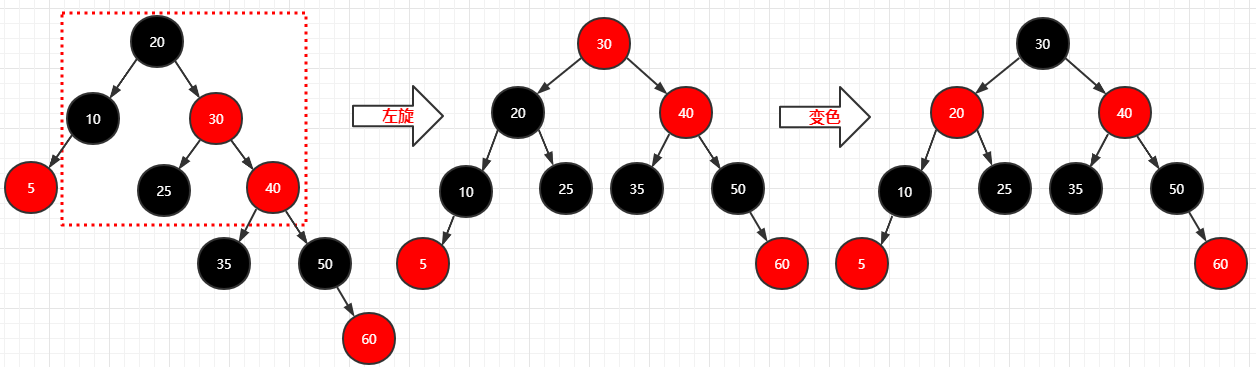
source-12

1
2
3
4
5
步骤：
1.在上面步骤的基础上，达到了子树是一颗红黑树
2.然后把变色的结点（40）当做是一个新节点，插入到红框中的树中
3.在这种情况下进行红框树的调整
4.先左旋，结点重连，然后旋转的节点和中心节点变色

再插入个结点（6）

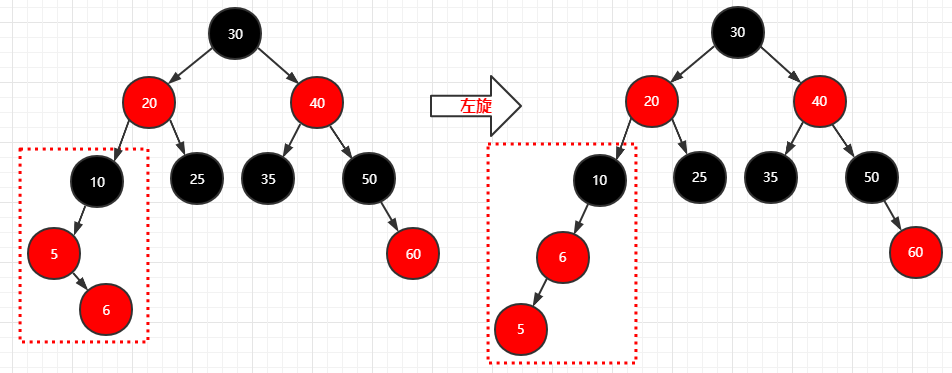
source-13

1
2
步骤：
1.(5)结点以(6)为中心，进行左旋

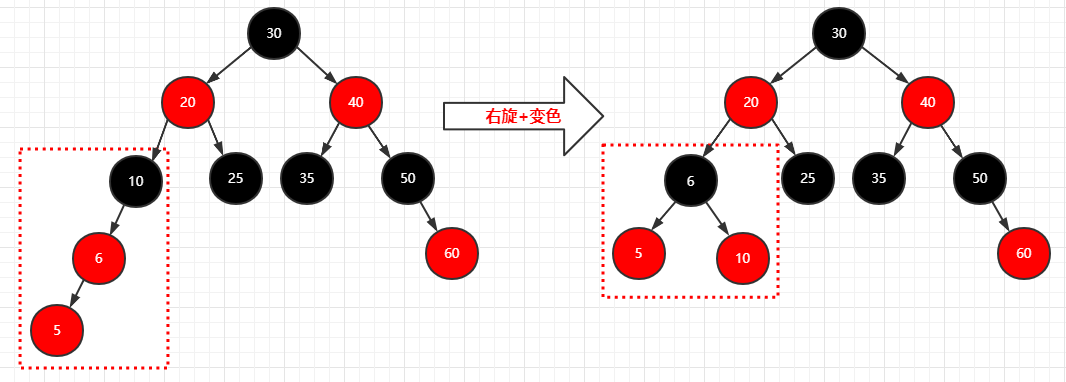
source-14

1
2
3
步骤：
2.然后就和上文插入(60)结点步骤相同
3.先进行右旋，然后变色

总结

当插入一个新节点（红色）时：

父节点是黑色的，不用进行调整

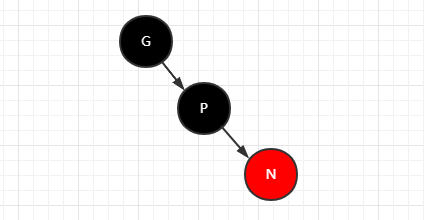
source-07

父节点是红色的，并且

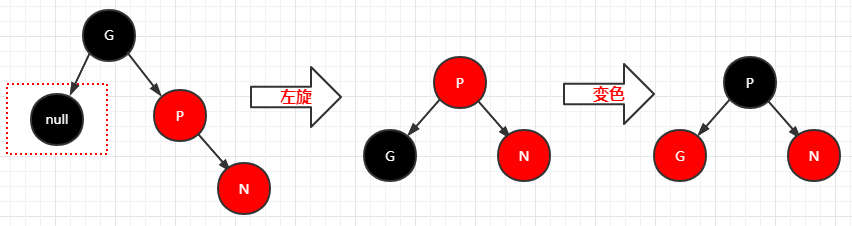
1.叔叔是空的，旋转+变色

source-08

2.叔叔是红色，父节点+叔叔节点变黑色，祖父节点变红色

source-10

3.叔叔是黑色，旋转+变色

source-12

源码

树化条件
1
2
3
4
5
6
//当链表长度达到阈值8时，转换成红黑树
static final int TREEIFY_THRESHOLD = 8;
//满足树化的最小数组长度
static final int MIN_TREEIFY_CAPACITY = 64;
//当扩容红黑树拆分链表后判断其数量是否大于6，大于则重组红黑树
static final int UNTREEIFY_THRESHOLD = 6;
红黑树存储结构-TreeNode
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//红黑树存储结构对象
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
    //父节点
    TreeNode<K,V> parent;  // red-black tree links
    //左子节点
    TreeNode<K,V> left;
    //右子节点
    TreeNode<K,V> right;
    //双向链表的前一个结点
    TreeNode<K,V> prev;    // needed to unlink next upon deletion
    //颜色
    boolean red;
    //继承Node得到，双向链表的下一个结点
    //Node<K,V> next;
}

//TreeNode继承的LinkedHashMap.Entry
static class Entry<K,V> extends HashMap.Node<K,V> {
    Entry<K,V> before, after;
    Entry(int hash, K key, V value, Node<K,V> next) {
        super(hash, key, value, next);
    }
}
//LinkedHashMap.Entry继承Map.Entry<K,V>
static class Node<K,V> implements Map.Entry<K,V> {
    final int hash;
    final K key;
    V value;
    Node<K,V> next;
}

所以说，上文TreeNode实际上是Node的子类，它有着两个属性，一个next，一个prev，也就是说，TreeNode还是一个双向链表。

添加元素
1
2
3
public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}
1
2
3
4
static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

由于JDK1.8的HashMap有了红黑树的保障，所以相对于计算Hash值没有JDK1.7那么复杂。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
               boolean evict) {
    Node<K,V>[] tab; Node<K,V> p; int n, i;
    if ((tab = table) == null || (n = tab.length) == 0)
		//对数组初始化或扩容
        n = (tab = resize()).length;
    //(n - 1) & hash 计算数组下标
    if ((p = tab[i = (n - 1) & hash]) == null)
        tab[i] = newNode(hash, key, value, null);
    else {
        Node<K,V> e; K k;
        //如果头结点的key等于插入的key，赋值给e
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
            e = p;
        //如果P是个红黑树
        else if (p instanceof TreeNode)
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
        else {
            //如果P是个链表，HashMap默认
            for (int binCount = 0; ; ++binCount) {
                if ((e = p.next) == null) {
                    //使用尾插法插入链表尾部
                    p.next = newNode(hash, key, value, null);
                    //当插入第九个元素时，调用树化方法
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                        treeifyBin(tab, hash);
                    break;
                }
                //当插入的数据刚好落在链表中时
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e;
            }
        }
        //判断是否要更新，并且返回旧值
        if (e != null) { // existing mapping for key
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e);
            return oldValue;
        }
    }
    ++modCount;
    //自增size后判断是否超过扩容因子（JDK1.7时还有判断当前链表是否有元素）
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict);
    return null;
}
链表树化
数组扩容或构建双向链表

在JDK1.7中，采用头插法插入到链表的头部，而在JDK1.8中，采用的是尾插法插入到链表中，并且当链表的数量大于8时，也就是添加第九个元素时，会调用树化方法treeifyBin，根据条件将链表转换成红黑树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//链表树化红黑树
final void treeifyBin(Node<K,V>[] tab, int hash) {
    int n, index; Node<K,V> e;
    //如果当前数组为空 或者 数组长度小于64时
    if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
        //对数组进行扩容
        resize();
    else if ((e = tab[index = (n - 1) & hash]) != null) {
        TreeNode<K,V> hd = null, tl = null;
        //遍历链表
        do {
            //把Node类型转换成红黑树的TreeNode类型
            TreeNode<K,V> p = replacementTreeNode(e, null);
            //缓存头结点
            if (tl == null)
                hd = p;
            else {
                //建立双向链表关系
                p.prev = tl;
                tl.next = p;
            }
            tl = p;
        } while ((e = e.next) != null);
        if ((tab[index] = hd) != null)
            //hd作为链表的头结点，也是红黑树的根节点，遍历链表把其他数值逐个插入到红黑树中
            hd.treeify(tab);
    }
}
1
2
3
4
//把Node类型转换成TreeNode类型
TreeNode<K,V> replacementTreeNode(Node<K,V> p, Node<K,V> next) {
    return new TreeNode<>(p.hash, p.key, p.value, next);
}

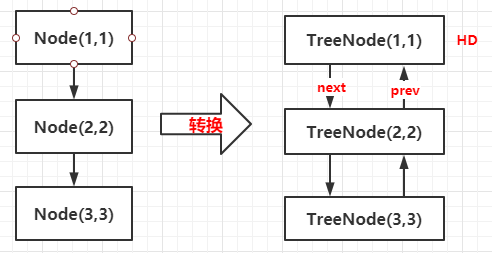
source-20

真正树化

接下来是真正的将链表树化的逻辑方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
final void treeify(Node<K,V>[] tab) {
    TreeNode<K,V> root = null;
    //this（链表的头结点），开始遍历
    for (TreeNode<K,V> x = this, next; x != null; x = next) {
        //获取链表的下一个结点
        next = (TreeNode<K,V>)x.next;
        //设置结点左右子结点都是NULL
        x.left = x.right = null;
        //如果root根节点对象等于null，则赋值root根节点对象，并且变黑色
        if (root == null) {
            x.parent = null;
            x.red = false;
            root = x;
        }
        else {
            //新增结点的Key的值
            K k = x.key;
            //新增结点的hash值
            int h = x.hash;
            //Key的数据类型
            Class<?> kc = null;
            for (TreeNode<K,V> p = root;;) {
                int dir, ph;
                //根节点的key值
                K pk = p.key;
                //如果根结点的hash值大于新增结点的hash值，则放在左树上（dir = -1）代表左边
                if ((ph = p.hash) > h)
                    dir = -1;
                //否则放在右边
                else if (ph < h)
                    dir = 1;
                //如果hash值相同，获取key的数据类型，判断是否实现Comparable接口，则调用实现的compareTo方法
                //如果compareTo还相同或者没实现Compareable接口，则调用tieBreakOrder
                else if ((kc == null &&
                          (kc = comparableClassFor(k)) == null) ||
                         (dir = compareComparables(kc, k, pk)) == 0)
                    //比较getClass().getName() 和 System.identityHashCode
                    dir = tieBreakOrder(k, pk);
				
                //一直遍历直到想放的位置没有结点，等于 null
                TreeNode<K,V> xp = p;
                if ((p = (dir <= 0) ? p.left : p.right) == null) {
                    //赋值新节点x的父节点
                    x.parent = xp;
                    //如果左边放左边，如果右边放右边
                    if (dir <= 0)
                        xp.left = x;
                    else
                        xp.right = x;
                    //执行插入红黑树过程
                    root = balanceInsertion(root, x);
                    break;
                }
            }
        }
    }
    //把根节点存储到数组中,并且把红黑树的根节点设置成双向链表的根节点
    moveRootToFront(tab, root);
}
根节点移动到双向链表头部
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {
    int n;
    if (root != null && tab != null && (n = tab.length) > 0) {
        int index = (n - 1) & root.hash;
        TreeNode<K,V> first = (TreeNode<K,V>)tab[index];
        if (root != first) {
            Node<K,V> rn;
            //把红黑树的根节点赋值在数组上
            tab[index] = root;
            //获取红黑树的根节点在双向链表中的前一个结点rp
            TreeNode<K,V> rp = root.prev;
            //如果红黑树根节点在双线链表中的下一个结点rn不为空
            if ((rn = root.next) != null)
                //下一个结点的prev指向rp（等于跳过了root）
                ((TreeNode<K,V>)rn).prev = rp;
            //如果上一个结点rp不为空，它的next指向rn（等于跳过了root）
            if (rp != null)
                rp.next = rn;
            //如果原数组中的存储的链表头结点不为空，则通过头插法，把root插入到first之上
            if (first != null)
                first.prev = root;
            root.next = first;
            root.prev = null;
        }
        assert checkInvariants(root);
    }
}
红黑树添加新节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
                               int h, K k, V v) {
    Class<?> kc = null;
    boolean searched = false;
    TreeNode<K,V> root = (parent != null) ? root() : this;
    for (TreeNode<K,V> p = root;;) {
        int dir, ph; K pk;
        if ((ph = p.hash) > h)
            dir = -1;
        else if (ph < h)
            dir = 1;
        else if ((pk = p.key) == k || (k != null && k.equals(pk)))
            return p;
        else if ((kc == null &&
                  (kc = comparableClassFor(k)) == null) ||
                 (dir = compareComparables(kc, k, pk)) == 0) {
            if (!searched) {
                TreeNode<K,V> q, ch;
                searched = true;
                //查找key是否属于红黑树中
                if (((ch = p.left) != null &&
                     (q = ch.find(h, k, kc)) != null) ||
                    ((ch = p.right) != null &&
                     (q = ch.find(h, k, kc)) != null))
                    return q;
            }
            dir = tieBreakOrder(k, pk);
        }

        TreeNode<K,V> xp = p;
        if ((p = (dir <= 0) ? p.left : p.right) == null) {
            Node<K,V> xpn = xp.next;
            TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
            if (dir <= 0)
                xp.left = x;
            else
                xp.right = x;
            xp.next = x;
            x.parent = x.prev = xp;
            if (xpn != null)
                ((TreeNode<K,V>)xpn).prev = x;
            moveRootToFront(tab, balanceInsertion(root, x));
            return null;
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
/* 
  红黑树的插入逻辑
  @Params
  root 	根节点
  x		即将插入的结点
*/
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
                                            TreeNode<K,V> x) {
    //新节点默认为红色
    x.red = true;
    //xp表示父节点，xpp表示x的祖父节点，xppl表示xpp的左孩子结点，xppr表示xpp的右孩子结点
    for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
        //如果x没有父节点，则表示x是第一个结点，自动成为根节点，根节点为黑色
        if ((xp = x.parent) == null) {
            x.red = false;
            return x;
        }
        //如果父节点是黑色的，不需要做调整
        else if (!xp.red || (xpp = xp.parent) == null)
            return root;
        //上面逻辑已经处理了父节点是黑色的情况，所以下面的逻辑父节点一定是红色的
        //当新节点的父节点是xpp的左叶子节点时
        if (xp == (xppl = xpp.left)) {
            //叔叔节点不为空 且 叔叔节点等于红色
            if ((xppr = xpp.right) != null && xppr.red) {
                //叔叔节点变黑色
                xppr.red = false;
                //父节点变黑色
                xp.red = false;
                //祖父节点变红色
                xpp.red = true;
                //子树调整完成，可能需要递归调整，把祖父节点赋值给x，递归调整
                x = xpp;
            }
            //进入else语句 叔叔节点为空或者等于黑色
            else {
                
                //当新节点落在父节点的右边时
                if (x == xp.right) {
                    root = rotateLeft(root, x = xp);
                    //重新赋值xp 和xpp的值
                    xpp = (xp = x.parent) == null ? null : xp.parent;
                }
                //如果xp（也就是之前插入的新节点）不为null
                if (xp != null) {
                    //把xp变成黑色
                    xp.red = false;
                    //祖父节点不为null时，变成红色
                    if (xpp != null) {
                        xpp.red = true;
                        //进行右旋
                        root = rotateRight(root, xpp);
                    }
                }
            }
        }
        else {
            //当新节点的父节点是xpp的右叶子节点，且它的叔叔节点不为空且红色
            if (xppl != null && xppl.red) {
                xppl.red = false;
                xp.red = false;
                xpp.red = true;
                x = xpp;
            }
            else {
                if (x == xp.left) {
                    root = rotateRight(root, x = xp);
                    xpp = (xp = x.parent) == null ? null : xp.parent;
                }
                if (xp != null) {
                    xp.red = false;
                    if (xpp != null) {
                        xpp.red = true;
                        root = rotateLeft(root, xpp);
                    }
                }
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//左旋
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
                                      TreeNode<K,V> p) {
    TreeNode<K,V> r, pp, rl;
    //如果新增的父节点p不等于null且 p的右子结点（新增节点） 不等于null
    //1.r = p.right （把新增节点赋值给 r）
    if (p != null && (r = p.right) != null) {
        //2.p.right = r.left解释：
        //新增的节点r.left默认为null ，将null 赋值给 p.right，等于取消p对r的指针
        //rl != null 时主要用于递归父树左旋
        if ((rl = p.right = r.left) != null)
            rl.parent = p;
        //3.r.parent = p.parent
        //将新增的节点r.parent指向p.parent上，也就是新增节点的祖父节点pp
        if ((pp = r.parent = p.parent) == null)
            //如果等于根节点，赋值黑色
            (root = r).red = false;
        //用于定位p节点处于pp节点的左侧还是右侧，然后断开pp对p的指向，修改成pp对r的指向
        //如果父节点落在祖父节点的左边
        else if (pp.left == p)
            //把r当做pp的左叶子节点
            pp.left = r;
        //如果父节点落在祖父节点的右边
        else
            //把r当做pp右叶子节点
            pp.right = r;
        //把p当做r的左叶子节点
        r.left = p;
        p.parent = r;
    }
    return root;
}

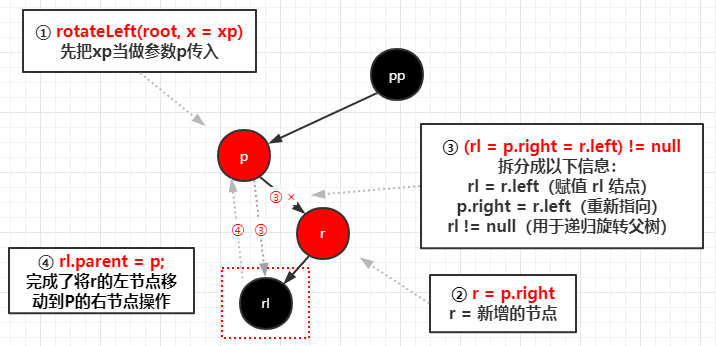
source-15

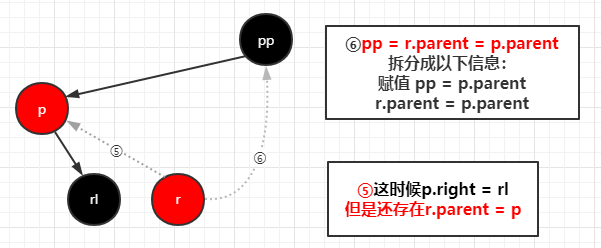
source-16

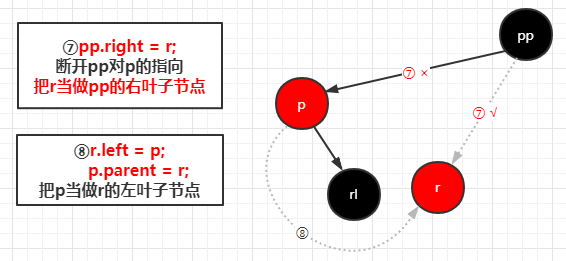
source-17

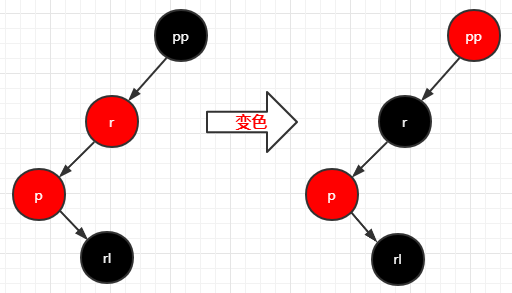
source-18

完成左旋之后进行变色，变完色之后右旋

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//通过调用  root = rotateLeft(root, xpp); 所以参数 p = xpp
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
                                       TreeNode<K,V> p) {
    TreeNode<K,V> l, pp, lr;
    //祖父节点p和它的左子节点l不为空
    if (p != null && (l = p.left) != null) {
        //用于右旋之后节点分配
        if ((lr = p.left = l.right) != null)
            lr.parent = p;
        //如果祖父节点p是根节点，则p.parent等于null，右旋之后，l将作为根节点，所以变色黑色
        if ((pp = l.parent = p.parent) == null)
            (root = l).red = false;
        //如果祖父节点p不是根节点，则获取p的父节点pp，右旋之后，pp指向l
        else if (pp.right == p)
            pp.right = l;
        else
            pp.left = l;
        //把p作为l的右结点
        l.right = p;
        p.parent = l;
    }
    return root;
}

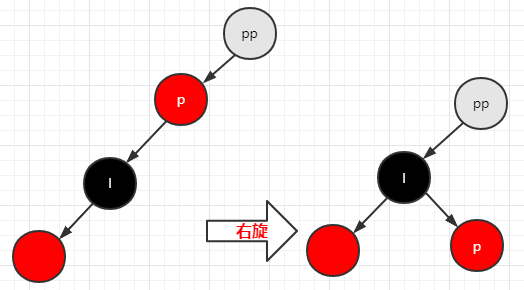
source-19

扩容

再看一下扩容方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
final Node<K,V>[] resize() {
    Node<K,V>[] oldTab = table;
    int oldCap = (oldTab == null) ? 0 : oldTab.length;
    int oldThr = threshold;
    int newCap, newThr = 0;
    if (oldCap > 0) {
        if (oldCap >= MAXIMUM_CAPACITY) {
            threshold = Integer.MAX_VALUE;
            return oldTab;
        }
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                 oldCap >= DEFAULT_INITIAL_CAPACITY)
            //扩容，长度左移
            newThr = oldThr << 1; // double threshold
    }
    else if (oldThr > 0) // initial capacity was placed in threshold
        newCap = oldThr;
    else {               // zero initial threshold signifies using defaults
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
    if (newThr == 0) {
        //新数组的大小乘以扩容因子
        float ft = (float)newCap * loadFactor;
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                  (int)ft : Integer.MAX_VALUE);
    }
    threshold = newThr;
    @SuppressWarnings({"rawtypes","unchecked"})
    Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
    table = newTab;
    //如果老数组不为空，也就是扩容逻辑
    if (oldTab != null) {
        for (int j = 0; j < oldCap; ++j) {
            Node<K,V> e;
            if ((e = oldTab[j]) != null) {
                oldTab[j] = null;
                //如果链表上只有一个元素，直接移动过去并且赋值到数组中
                if (e.next == null)
                    newTab[e.hash & (newCap - 1)] = e;
                //如果数组上的是红黑树
                else if (e instanceof TreeNode)
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                else { // preserve order
                    Node<K,V> loHead = null, loTail = null;
                    Node<K,V> hiHead = null, hiTail = null;
                    Node<K,V> next;
                    //链表转移，使用尾插法，链表元素的hash值&旧数组长度，等于0的元素转移到lo链表、其余的元素转移到hi链表，最终newTab[j] = loHead、newTab[j + oldCap] = hiHead完成链表扩容
                    do {
                        next = e.next;
                        //hash值和原数组长度相与，等于0原数组
                        if ((e.hash & oldCap) == 0) {
                            //赋值低位index的头结点
                            if (loTail == null)
                                loHead = e;
                            else
                                //链接低位index的结点
                                loTail.next = e;
                            //更新末尾结点
                            loTail = e;
                        }
                        else {
                             //赋值高位index的头结点
                            if (hiTail == null)
                                hiHead = e;
                            else
                                //链接高位index的结点
                                hiTail.next = e;
                            //更新末尾结点
                            hiTail = e;
                        }
                    } while ((e = next) != null);
                    //链表赋值到数组的低位index中
                    if (loTail != null) {
                        loTail.next = null;
                        newTab[j] = loHead;
                    }
                     //链表赋值到数组的高位index中
                    if (hiTail != null) {
                        hiTail.next = null;
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    return newTab;
}
链表扩容

​ 链表转移，使用尾插法，链表元素的hash值&旧数组长度，等于0的元素转移到lo链表、其余的元素转移到hi链表，最终newTab[j] = loHead、newTab[j + oldCap] = hiHead完成链表扩容

红黑树扩容

​ 遍历数组，获取数组上的红黑树root节点进行操作，树节点（treeNode）存在双向链表结构，使用next指针如链表转移一般进行操作，构建高低位链表，记录高位、低位节点个数，头部节点放入数组索引位置

a、节点个数如果小于6则结构改回单向链表（TreeNode->Node）
b、大于6个，如果高低位链表仅存在一个，不需要额外操作，因为整棵树已经迁移；如果两个都存在，重新进行树化
c、tab[index] = loHead，tab[index + bit] = hiHead

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
    //数组上的红黑树根节点
    TreeNode<K,V> b = this;
    // Relink into lo and hi lists, preserving order
    TreeNode<K,V> loHead = null, loTail = null;
    TreeNode<K,V> hiHead = null, hiTail = null;
    int lc = 0, hc = 0;
    //遍历红黑树的双向链表
    for (TreeNode<K,V> e = b, next; e != null; e = next) {
        next = (TreeNode<K,V>)e.next;
        e.next = null;
        if ((e.hash & bit) == 0) {
            if ((e.prev = loTail) == null)
                loHead = e;
            else
                loTail.next = e;
            loTail = e;
            //计数低位index的链表的个数
            ++lc;
        }
        else {
            if ((e.prev = hiTail) == null)
                hiHead = e;
            else
                hiTail.next = e;
            hiTail = e;
            //计数高位index的链表的个数
            ++hc;
        }
    }
	//拆分成两个链表之后，比较
    if (loHead != null) {
        //如果链表长度<=6
        if (lc <= UNTREEIFY_THRESHOLD)
            //退化成链表赋值到数组中
            tab[index] = loHead.untreeify(map);
        else {
            //当hiHead == null时，则等于红黑树不需要拆分，直接把整棵树（也就是根节点）移动到数组上
            tab[index] = loHead;
            //hiHead不为空时，对低位链表进行树化，整个链表重新创建红黑树
            if (hiHead != null) // (else is already treeified)
                loHead.treeify(tab);
        }
    }
    //以下逻辑和低位链表逻辑相同
    if (hiHead != null) {
        if (hc <= UNTREEIFY_THRESHOLD)
            //新数组下标 = 原数组下标 + 原数组长度
            tab[index + bit] = hiHead.untreeify(map);
        else {
            tab[index + bit] = hiHead;
            if (loHead != null)
                hiHead.treeify(tab);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
//遍历双向链表，把TreeNode类型转换成Node类型，建立单向链表，返回头结点
final Node<K,V> untreeify(HashMap<K,V> map) {
    Node<K,V> hd = null, tl = null;
    for (Node<K,V> q = this; q != null; q = q.next) {
        Node<K,V> p = map.replacementNode(q, null);
        if (tl == null)
            hd = p;
        else
            tl.next = p;
        tl = p;
    }
    return hd;
}
get方法
1
2
3
4
public V get(Object key) {
    Node<K,V> e;
    return (e = getNode(hash(key), key)) == null ? null : e.value;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
final Node<K,V> getNode(int hash, Object key) {
    Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
    if ((tab = table) != null && (n = tab.length) > 0 &&
        (first = tab[(n - 1) & hash]) != null) {
        if (first.hash == hash && // always check first node
            //如果刚好等于根节点，返回
            ((k = first.key) == key || (key != null && key.equals(k))))
            return first;
        if ((e = first.next) != null) {
            //如果它是红黑树，则调用红黑树的查找算法
            if (first instanceof TreeNode)
                return ((TreeNode<K,V>)first).getTreeNode(hash, key);
            do {
                //否则循环链表查找
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    return e;
            } while ((e = e.next) != null);
        }
    }
    return null;
}
1
2
3
final TreeNode<K,V> getTreeNode(int h, Object k) {
    return ((parent != null) ? root() : this).find(h, k, null);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/*
* h: get的Key的hash值
* k: get的key
*/
final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
    TreeNode<K,V> p = this;
    do {
        int ph, dir; K pk;
        TreeNode<K,V> pl = p.left, pr = p.right, q;
        //判断hash在左边
        if ((ph = p.hash) > h)
            p = pl;
        //在右边
        else if (ph < h)
            p = pr;
        //相等且key相同，返回节点
        else if ((pk = p.key) == k || (k != null && k.equals(pk)))
            return p;
        //如果左边等于null直接找右边
        else if (pl == null)
            p = pr;
        //如果右边等于null直接找右边
        else if (pr == null)
            p = pl;
        //如果key自定义了比较算法，compare之类的判断走哪一边
        else if ((kc != null ||
                  (kc = comparableClassFor(k)) != null) &&
                 (dir = compareComparables(kc, k, pk)) != 0)
            p = (dir < 0) ? pl : pr;
        //否则递归查询
        else if ((q = pr.find(h, k, kc)) != null)
            return q;
        else
            p = pl;
    } while (p != null);
    return null;
}

ConcurrentHashMap

1
2
3
4
5
6
7
8
9
10
11
12
13
//表示当前的整个ConcurrentHashMap正在扩容
static final int MOVED     = -1;
//创建数组时用于Cas操作，设置成 -1 则代表CAS操作成功，然后创建数组，计算扩容的阈值并赋值到sizeCtl上
private transient volatile int sizeCtl;

//ConcurrentHashMap中元素的最大值 2的31次方
private static final int MAXIMUM_CAPACITY = 1 << 30;

//当扩容数组时，待迁移的数组长度值
private transient volatile int transferIndex;

//存储扩容时的数组，用以迁移新旧数据
private transient volatile Node<K,V>[] nextTable;
红黑树结构对象-TreeBin
1
2
3
4
5
6
7
8
9
10
11
12
//把整个红黑树结构封在TreeBin对象中
static final class TreeBin<K,V> extends Node<K,V> {\
    //红黑树的根节点
    TreeNode<K,V> root;
    volatile TreeNode<K,V> first;
    volatile Thread waiter;
    volatile int lockState;
    // values for lockState
    static final int WRITER = 1; // set while holding write lock
    static final int WAITER = 2; // set when waiting for write lock
    static final int READER = 4; // increment value for setting read lock
}

ConcurrentHashMap的数组中将存储Node类型和TreeBin类型，TreeBin用于承载红黑树的整个结构，其中有一个root属性存储红黑树的根节点。

这样做的目的是为了后面对红黑树根节点加锁时，直接对TreeBin对象加锁，可以不用考虑在加锁的过程中，红黑树的根节点变化情况。

添加元素
1
2
3
public V put(K key, V value) {
    return putVal(key, value, false);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
final V putVal(K key, V value, boolean onlyIfAbsent) {
    if (key == null || value == null) throw new NullPointerException();
    int hash = spread(key.hashCode());
    int binCount = 0;
    for (Node<K,V>[] tab = table;;) {
        Node<K,V> f; int n, i, fh;
        //初始化数组
        if (tab == null || (n = tab.length) == 0)
            tab = initTable();
        //获取数组下标的Node对象并赋值到f中，并判断是否为空
        else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) {
            //通过cas操作赋值到数组下标中，如果失败则重新循环（就不会再进到这个条件了，因为数组下标内容已经不为空）
            if (casTabAt(tab, i, null,
                         new Node<K,V>(hash, key, value, null)))
                break;                   // no lock when adding to empty bin
        }
        //如果ConcurrentHashMap正在扩容，则帮助它进行扩容
        else if ((fh = f.hash) == MOVED)
            tab = helpTransfer(tab, f);
        else {
            V oldVal = null;
            //对链表/红黑树的头节点加锁
            synchronized (f) {
                //判断加完锁之后头结点是否还是f（避免加锁时被修改了）
                if (tabAt(tab, i) == f) {
                    //如果是链表
                    if (fh >= 0) {
                        //统计链表长度
                        binCount = 1;
                        //遍历链表，插入
                        for (Node<K,V> e = f;; ++binCount) {
                            K ek;
                            if (e.hash == hash &&
                                ((ek = e.key) == key ||
                                 (ek != null && key.equals(ek)))) {
                                oldVal = e.val;
                                if (!onlyIfAbsent)
                                    e.val = value;
                                break;
                            }
                            Node<K,V> pred = e;
                            //尾插法
                            if ((e = e.next) == null) {
                                pred.next = new Node<K,V>(hash, key,
                                                          value, null);
                                break;
                            }
                        }
                    }
                    else if (f instanceof TreeBin) {
                        Node<K,V> p;
                        binCount = 2;
                        if ((p = ((TreeBin<K,V>)f).putTreeVal(hash, key,
                                                              value)) != null) {
                            oldVal = p.val;
                            if (!onlyIfAbsent)
                                p.val = value;
                        }
                    }
                }
            }

            if (binCount != 0) {
                //如果链表长度大于8，则进行树化
                if (binCount >= TREEIFY_THRESHOLD)
                    treeifyBin(tab, i);
                if (oldVal != null)
                    return oldVal;
                break;
            }
        }
    }
    //添加元素，总元素数量加1
    addCount(1L, binCount);
    return null;
}
初始化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
private final Node<K,V>[] initTable() {
    Node<K,V>[] tab; int sc;
    while ((tab = table) == null || tab.length == 0) {
        if ((sc = sizeCtl) < 0)
            //放弃对CPU资源的控制，再和其他线程竞争CPU资源
            Thread.yield(); // lost initialization race; just spin
        //CAS对sizeCtl减1，如果成功则创建tab数组
        else if (U.compareAndSwapInt(this, SIZECTL, sc, -1)) {
            try {
                if ((tab = table) == null || tab.length == 0) {
                    int n = (sc > 0) ? sc : DEFAULT_CAPACITY;
                    @SuppressWarnings("unchecked")
                    Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n];
                    table = tab = nt;
                    // 16 - 4 = 12 扩容阈值
                    sc = n - (n >>> 2);
                }
            } finally {
                //赋值扩容阈值
                sizeCtl = sc;
            }
            break;
        }
    }
    return tab;
}
树化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
private final void treeifyBin(Node<K,V>[] tab, int index) {
    Node<K,V> b; int n, sc;
    if (tab != null) {
        if ((n = tab.length) < MIN_TREEIFY_CAPACITY)
            tryPresize(n << 1);
        else if ((b = tabAt(tab, index)) != null && b.hash >= 0) {
            //树化前加锁链表头结点
            synchronized (b) {
                if (tabAt(tab, index) == b) {
                    TreeNode<K,V> hd = null, tl = null;
                    //改成双向链表
                    for (Node<K,V> e = b; e != null; e = e.next) {
                        TreeNode<K,V> p =
                            new TreeNode<K,V>(e.hash, e.key, e.val,
                                              null, null);
                        if ((p.prev = tl) == null)
                            //链表头结点
                            hd = p;
                        else
                            tl.next = p;
                        tl = p;
                    }
                    //通过TreeBin的构造方法创建红黑树并赋值到数组上
                    setTabAt(tab, index, new TreeBin<K,V>(hd));
                }
            }
        }
    }
}
计数
1
2
3
4
5
6
7
8
9
10
11
12
13
//用于累加计数元素数量
private transient volatile long baseCount;

//用于分治对baseCount进行CAS失败后的资源竞争，等同于LongAdder的计算思想
private transient volatile CounterCell[] counterCells;

//用于创建CounterCell数组时加锁的状态位
private transient volatile int cellsBusy;

@sun.misc.Contended static final class CounterCell {
    volatile long value;
    CounterCell(long x) { value = x; }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
//x 表示需要增加的值
//通过CAS对baseCount进行累加操作，若CAS失败，则退而求其次，将累加的值累加到CounterCell篮子里
//避免了多线程情况下对同一个资源竞争，分治，一个资源分散成多个资源CAS
//复制了LongAdder的写法
private final void addCount(long x, int check) {
    CounterCell[] as; long b, s;
    //如果CounterCell数组非空  或  CAS修改BaseCount失败时进入下面逻辑
    if ((as = counterCells) != null ||
        !U.compareAndSwapLong(this, BASECOUNT, b = baseCount, s = b + x)) {
        CounterCell a; long v; int m;
        boolean uncontended = true;
        //满足条件：1.[as == null] 或者 2.[长度小于0] 或者 3.[对应下标的CounterCell对象为空]
        if (as == null || (m = as.length - 1) < 0 ||
            //下标计算规则：随机数 & as.length - 1
            (a = as[ThreadLocalRandom.getProbe() & m]) == null ||
            //上面的条件均不满足时，也就是CounterCell对象不为空，则将执行第四个逻辑分支
            //4.对CounterCell里的值进行CAS累加
            !(uncontended =
              U.compareAndSwapLong(a, CELLVALUE, v = a.value, v + x))) {
            
            //若上面四个分支条件有一个满足，则进入这个方法
            //进行数组初始化、CounterCell对象初始化、累加x
            fullAddCount(x, uncontended);
            return;
        }
        if (check <= 1)
            return;
        s = sumCount();
    }
    //当累加操作成功执行后，进入扩容检查逻辑
    //小于0（delete操作）则跳过，大于等于0（add操作）则开启扩容检查
    if (check >= 0) {
        Node<K,V>[] tab, nt; int n, sc;
        //当元素大小大于扩容阈值，并且数组长度小于最大值 MAXIMUM_CAPACITY 时，进入扩容逻辑
        while (s >= (long)(sc = sizeCtl) && (tab = table) != null &&
               (n = tab.length) < MAXIMUM_CAPACITY) {
            int rs = resizeStamp(n);
            if (sc < 0) {
                if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 ||
                    sc == rs + MAX_RESIZERS || (nt = nextTable) == null ||
                    transferIndex <= 0)
                    break;
                if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1))
                    transfer(tab, nt);
            }
            //CAS将sc 改成一个很小的负数值
            else if (U.compareAndSwapInt(this, SIZECTL, sc,
                                         (rs << RESIZE_STAMP_SHIFT) + 2))
                //进入扩容逻辑，在该逻辑中会赋值nextTable属性
                transfer(tab, null);
            s = sumCount();
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
//x:累加值  wasUncontended: false 表示已经进行过CAS操作并且失败了
private final void fullAddCount(long x, boolean wasUncontended) {
    int h;
    //计算数组下标，ThreadLocalRandom.getProbe()同一个线程调用会得到相同的随机数
    if ((h = ThreadLocalRandom.getProbe()) == 0) {
        ThreadLocalRandom.localInit();      // force initialization
        h = ThreadLocalRandom.getProbe();
        wasUncontended = true;
    }
    boolean collide = false;                // True if last slot nonempty
    for (;;) {
        CounterCell[] as; CounterCell a; int n; long v;
        //当counterCells数组不为空时
        if ((as = counterCells) != null && (n = as.length) > 0) {
            //当对应index的CounterCell对象 == null时
            if ((a = as[(n - 1) & h]) == null) {
                //并且cellsBusy状态位为0时
                if (cellsBusy == 0) {
                    //初始化CounterCell对象
                    CounterCell r = new CounterCell(x); // Optimistic create
                    //通过CAS设置cellsBusy状态位
                    if (cellsBusy == 0 &&
                        U.compareAndSwapInt(this, CELLSBUSY, 0, 1)) {
                        boolean created = false;
                        try {
                            CounterCell[] rs; int m, j;
                            //若获得cellsBusy锁时，再进行doubleCheck
                            if ((rs = counterCells) != null &&
                                (m = rs.length) > 0 &&
                                rs[j = (m - 1) & h] == null) {
                                //赋值对象到数组中
                                rs[j] = r;
                                //设置创建状态
                                created = true;
                            }
                        } finally {
                            //重置锁状态位
                            cellsBusy = 0;
                        }
                        //创建状态成功时，跳出循环
                        if (created)
                            break;
                        //否则重新进入循环
                        continue;           // Slot is now non-empty
                    }
                }
                collide = false;
            }
            //CAS操作已经失败过了，则设置它为true，后续的重新循环就不走这个分支了
            else if (!wasUncontended)       // CAS already known to fail
                wasUncontended = true;      // Continue after rehash
            //对当前的CounterCell对象进行cas操作
            else if (U.compareAndSwapLong(a, CELLVALUE, v = a.value, v + x))
                break;
            //当数组和当前对象不符（有其他线程扩容过）或者大于CPU核心数，则把扩容标志位设置成false
            //目的是用来防止无限次扩容
            else if (counterCells != as || n >= NCPU)
                collide = false;            // At max size or stale
            //CAS失败或者cellsBusy被占用繁忙时，第一次循环会先进行重新计算index下标
            //当第二次循环依旧失败时，走到这个逻辑时，则设置扩容标志位等于true
            else if (!collide)
                collide = true;
            //第三次循环进来时，当扩容标志位等于ture时，进行CAS加锁并且扩容
            else if (cellsBusy == 0 &&
                     U.compareAndSwapInt(this, CELLSBUSY, 0, 1)) {
                try {
                    if (counterCells == as) {// Expand table unless stale
                        //数组扩容一倍
                        CounterCell[] rs = new CounterCell[n << 1];
                        for (int i = 0; i < n; ++i)
                            rs[i] = as[i];
                        counterCells = rs;
                    }
                } finally {
                    cellsBusy = 0;
                }
                collide = false;
                continue;                   // Retry with expanded table
            }
            //根据现有的下标重新计算一个新的下标并赋值到 h 上
            h = ThreadLocalRandom.advanceProbe(h);
        }
        //如果counterCells数组没有初始化，则对cellsBusy进行CAS赋值，类似于Lock状态位
        else if (cellsBusy == 0 && counterCells == as &&
                 U.compareAndSwapInt(this, CELLSBUSY, 0, 1)) {
            boolean init = false;
            try {                           // Initialize table
                //doubleCheck，判断依旧没初始化
                if (counterCells == as) {
                    //初始化CounterCell数组，赋值长度 = 2
                    CounterCell[] rs = new CounterCell[2];
                    //创建下标index = 1的CounterCell对象
                    rs[h & 1] = new CounterCell(x);
                    counterCells = rs;
                    //设置初始化成功标志位
                    init = true;
                }
            } finally {
                //初始化成功，重置状态位
                cellsBusy = 0;
            }
            //跳出死循环
            if (init)
                break;
        }
        //不满足上述所有分支时，或者多线程竞争cellsBusy失败时，就CAS竞争baseCount
        else if (U.compareAndSwapLong(this, BASECOUNT, v = baseCount, v + x))
            break;                          // Fall back on using base
    }
}
1
2
3
4
5
6
7
8
//用该对象占用在数组上，表示这个位置正在扩容
static final class ForwardingNode<K,V> extends Node<K,V> {
    final Node<K,V>[] nextTable;
    ForwardingNode(Node<K,V>[] tab) {
        super(MOVED, null, null, null);
        this.nextTable = tab;
    }
}
1
2
3
4
//在putval中，有一个分值逻辑代码是这样的，表示如果当前的f.hash == MOVED时，则进行帮助扩容逻辑
//也就是说，在putval的过程中，如果数组中的元素类型是ForwardingNode，则代表它正在扩容
else if ((fh = f.hash) == MOVED)
    tab = helpTransfer(tab, f);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//多线程进行扩容操作
final Node<K,V>[] helpTransfer(Node<K,V>[] tab, Node<K,V> f) {
    Node<K,V>[] nextTab; int sc;
    //判断数组元素类型，并且扩容数组nextTab是否产生
    if (tab != null && (f instanceof ForwardingNode) &&
        (nextTab = ((ForwardingNode<K,V>)f).nextTable) != null) {
        int rs = resizeStamp(tab.length);
        while (nextTab == nextTable && table == tab &&
               (sc = sizeCtl) < 0) {
            if ((sc >>> RESIZE_STAMP_SHIFT) != rs || sc == rs + 1 ||
                sc == rs + MAX_RESIZERS || transferIndex <= 0)
                break;
            //CAS对cs进行加1，sc在扩容时会被设置成一个负数，来一个线程扩容，该值就会加1
            if (U.compareAndSwapInt(this, SIZECTL, sc, sc + 1)) {
                transfer(tab, nextTab);
                break;
            }
        }
        return nextTab;
    }
    return table;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
//tab 原数组  , nextTab 新数组
//这里的扩容逻辑是从右往左，多线程并发扩容，每个线程依次获取某段长度=stride的数据进行扩容迁移
private final void transfer(Node<K,V>[] tab, Node<K,V>[] nextTab) {
    int n = tab.length, stride;
    //计算扩容的步长，多线程情况下，每个线程拾取相对步长的元素进行迁移，并发扩容
    if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE)
        stride = MIN_TRANSFER_STRIDE; // subdivide range
    //如果新数组等于null，则初始化新数组
    if (nextTab == null) {            // initiating
        try {
            //扩容一倍长度的数组对象
            @SuppressWarnings("unchecked")
            Node<K,V>[] nt = (Node<K,V>[])new Node<?,?>[n << 1];
            nextTab = nt;
        } catch (Throwable ex) {      // try to cope with OOME
            sizeCtl = Integer.MAX_VALUE;
            return;
        }
        //赋值到nextTable属性上
        nextTable = nextTab;
        //待迁移的数组长度
        transferIndex = n;
    }
    int nextn = nextTab.length;
    //创建一个标识正在扩容的对象
    ForwardingNode<K,V> fwd = new ForwardingNode<K,V>(nextTab);
    //标记当前线程是否具备继续往左进行数组元素迁移的能力（false表示正在迁移中）
    boolean advance = true;
    //标记当前线程是否已经完成了它自身所能够涉及到的数据迁移（我向左找不到了）
    boolean finishing = false; // to ensure sweep before committing nextTab
    for (int i = 0, bound = 0;;) {
        Node<K,V> f; int fh;
        while (advance) {
            int nextIndex, nextBound;
            //如果右下标大于左下标（表示有待迁移的数据,右下标自减一直缩），或者当前线程已经完成了扩容迁移
            if (--i >= bound || finishing)
                advance = false;
            //赋值nextIndex，并且判断是否有待处理的数组元素，若没有，则设置 i = -1
            else if ((nextIndex = transferIndex) <= 0) {
                i = -1;
                advance = false;
            }
            //CAS修改待迁移的数组长度，假设 transferIndex = 4， stride = 2的话
            else if (U.compareAndSwapInt
                     (this, TRANSFERINDEX, nextIndex,
                      //计算该线程的应该负责迁移数组元素的起始下标 通过计算得到 4 - 2 = 2
                      nextBound = (nextIndex > stride ?
                                   nextIndex - stride : 0))) {
                //表示当前线程需要负责的起始下标，若CAS成功，则赋值到bound = 2
                bound = nextBound;
                //表示当前线程需要负责的结束下标 4 - 1 = 3，所以最终该线程负责[2,3]区域
                i = nextIndex - 1;
                //获得待负责的区域了，设置状态false
                advance = false;
            }
        }
        //当上文逻辑判断没有待处理的数组元素时，i = -1 ，会进入当前分支
        if (i < 0 || i >= n || i + n >= nextn) {
            int sc;
            //当完成迁移了
            if (finishing) {
                nextTable = null;
                //将新的数组设置到旧的数组属性上
                table = nextTab;
                //重新设置扩容阈值
                sizeCtl = (n << 1) - (n >>> 1);
                return;
            }
            //当前线程执行完扩容操作，对sc进行自减
            if (U.compareAndSwapInt(this, SIZECTL, sc = sizeCtl, sc - 1)) {
                //判断当前的sc和之前计算的sc是否相等，若不等则有其他线程还在进行扩容操作，扩容还没完成
                if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT)
                    return;
                //若相等，则表示所有线程都已经扩容完成，设置完成标识位
                finishing = advance = true;
                i = n; // recheck before commit
            }
        }
        //如果当前位置的元素 == null
        else if ((f = tabAt(tab, i)) == null)
            //将ForwardingNode设置到 旧数组tab上，其他线程访问时判断是该对象类型，则会帮助扩容
            advance = casTabAt(tab, i, null, fwd);
        //若当前位置已经被迁移过了
        else if ((fh = f.hash) == MOVED)
            advance = true; // already processed
        else {
            //锁数组的头结点
            synchronized (f) {
                //doubleCheck
                if (tabAt(tab, i) == f) {
                    Node<K,V> ln, hn;
                    //链表的扩容逻辑，和JDK1.7的ConcurrentHashMap迁移一样
                    if (fh >= 0) {
                        int runBit = fh & n;
                        Node<K,V> lastRun = f;
                        for (Node<K,V> p = f.next; p != null; p = p.next) {
                            int b = p.hash & n;
                            if (b != runBit) {
                                runBit = b;
                                lastRun = p;
                            }
                        }
                        if (runBit == 0) {
                            ln = lastRun;
                            hn = null;
                        }
                        else {
                            hn = lastRun;
                            ln = null;
                        }
                        for (Node<K,V> p = f; p != lastRun; p = p.next) {
                            int ph = p.hash; K pk = p.key; V pv = p.val;
                            if ((ph & n) == 0)
                                ln = new Node<K,V>(ph, pk, pv, ln);
                            else
                                hn = new Node<K,V>(ph, pk, pv, hn);
                        }
                        setTabAt(nextTab, i, ln);
                        setTabAt(nextTab, i + n, hn);
                        //把旧数组的上的元素改成fwd对象
                        setTabAt(tab, i, fwd);
                        //设置true，继续往左走
                        advance = true;
                    }
                    //红黑树迁移逻辑，和JDK1.8的HashMap一样
                    else if (f instanceof TreeBin) {
                        TreeBin<K,V> t = (TreeBin<K,V>)f;
                        TreeNode<K,V> lo = null, loTail = null;
                        TreeNode<K,V> hi = null, hiTail = null;
                        int lc = 0, hc = 0;
                        for (Node<K,V> e = t.first; e != null; e = e.next) {
                            int h = e.hash;
                            TreeNode<K,V> p = new TreeNode<K,V>
                                (h, e.key, e.val, null, null);
                            if ((h & n) == 0) {
                                if ((p.prev = loTail) == null)
                                    lo = p;
                                else
                                    loTail.next = p;
                                loTail = p;
                                ++lc;
                            }
                            else {
                                if ((p.prev = hiTail) == null)
                                    hi = p;
                                else
                                    hiTail.next = p;
                                hiTail = p;
                                ++hc;
                            }
                        }
                        ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) :
                        (hc != 0) ? new TreeBin<K,V>(lo) : t;
                        hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) :
                        (lc != 0) ? new TreeBin<K,V>(hi) : t;
                        setTabAt(nextTab, i, ln);
                        setTabAt(nextTab, i + n, hn);
                        //把旧数组的上的元素改成fwd对象
                        setTabAt(tab, i, fwd);
                        //设置true，继续往左走
                        advance = true;
                    }
                }
            }
        }
    }
}

分析完添加元素和累加计数的分治方法之后，再看看统计元素大小的size方法：

1
2
3
4
5
6
public int size() {
    long n = sumCount();
    return ((n < 0L) ? 0 :
            (n > (long)Integer.MAX_VALUE) ? Integer.MAX_VALUE :
            (int)n);
}
1
2
3
4
5
6
7
8
9
10
11
12
//baseCount + CounterCell[] 的数据，累加起来就是总的Size
final long sumCount() {
    CounterCell[] as = counterCells; CounterCell a;
    long sum = baseCount;
    if (as != null) {
        for (int i = 0; i < as.length; ++i) {
            if ((a = as[i]) != null)
                sum += a.value;
        }
    }
    return sum;
}

“本篇文章主要摘自参考资料”